前置的知识这里只做提点,不详细展开,主要是为了告诉读者你需要哪些数学基础。读者最好能有一点离散数学的基础,如果发现下面的数学基础很多都不知道的话,可能需要补一些离散数学课,然后再来看这个教程。
集合是一堆确定的元素的全体,比如 A={1,2,3},B={train,bus,bicycle,airplane}。集合的元素可以是任何类型,不一定非得是数字。
一个元素要么属于一个集合,比如 1∈A;要么不属于一个集合,比如 ship∈/B。
集合的可以通过花括号里面罗列有限 (finite) 元素的方式来表示:
C={a,b,c,d,e,f,g,h,i,j,k}
在不产生歧义的情况下,我们可以使用省略号:
C={a,b,...,k}
集合也可以是无限 (infinite) 的:
S=2,4,6,...
也可以通过描述法来表示集合:
S={j:j>0∧j=2k,k>0}
或者
S={j:j is nonnegative and even}
其中,集合的表示需要注意的一个原则是表意明确,没有二义性。
我们常用全集 (universal set) U 来表示所有可能的元素,比如说 A={1,2,3,4,5},U={1,2,...,10}。
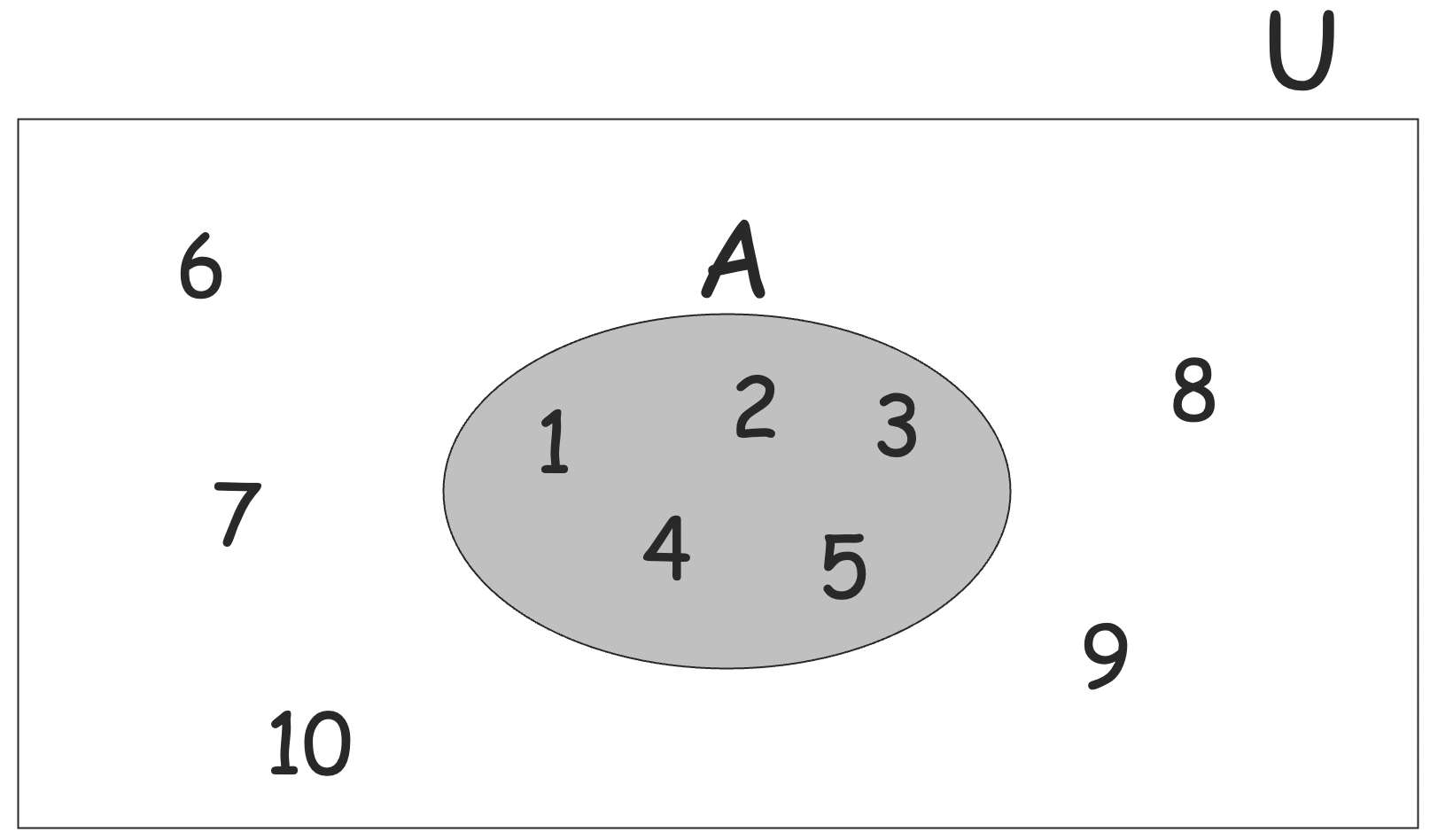
例如 A={1,2,3},B={2,3,4,5}
并集 (union)
- A∪B={1,2,3,4,5}
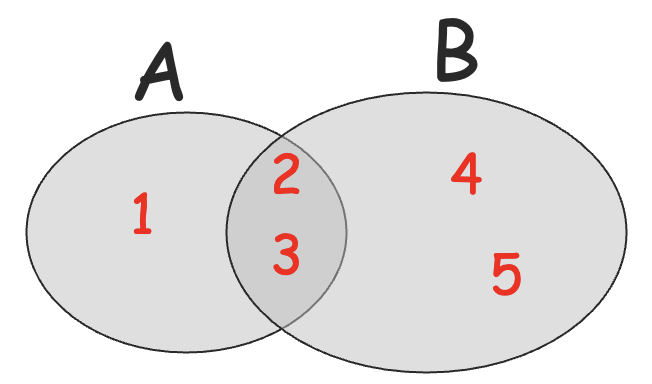
交集 (intersection)
- A∩B={2,3}
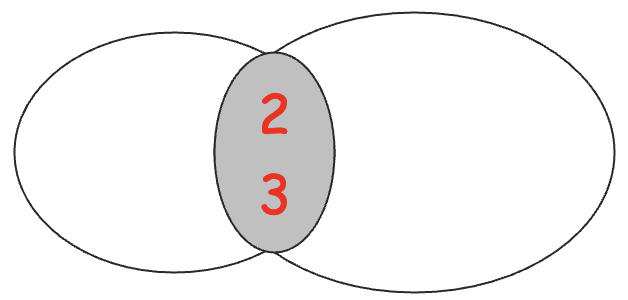
差集 (difference)
- A−B={1}
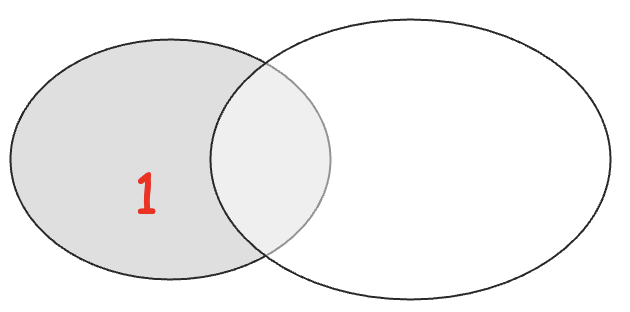
- B−A={4,5}
补集 (complement)
- 定义全集 U={1,..,7}
- A={1,2,3}⇒A=U−A={4,5,6,7}
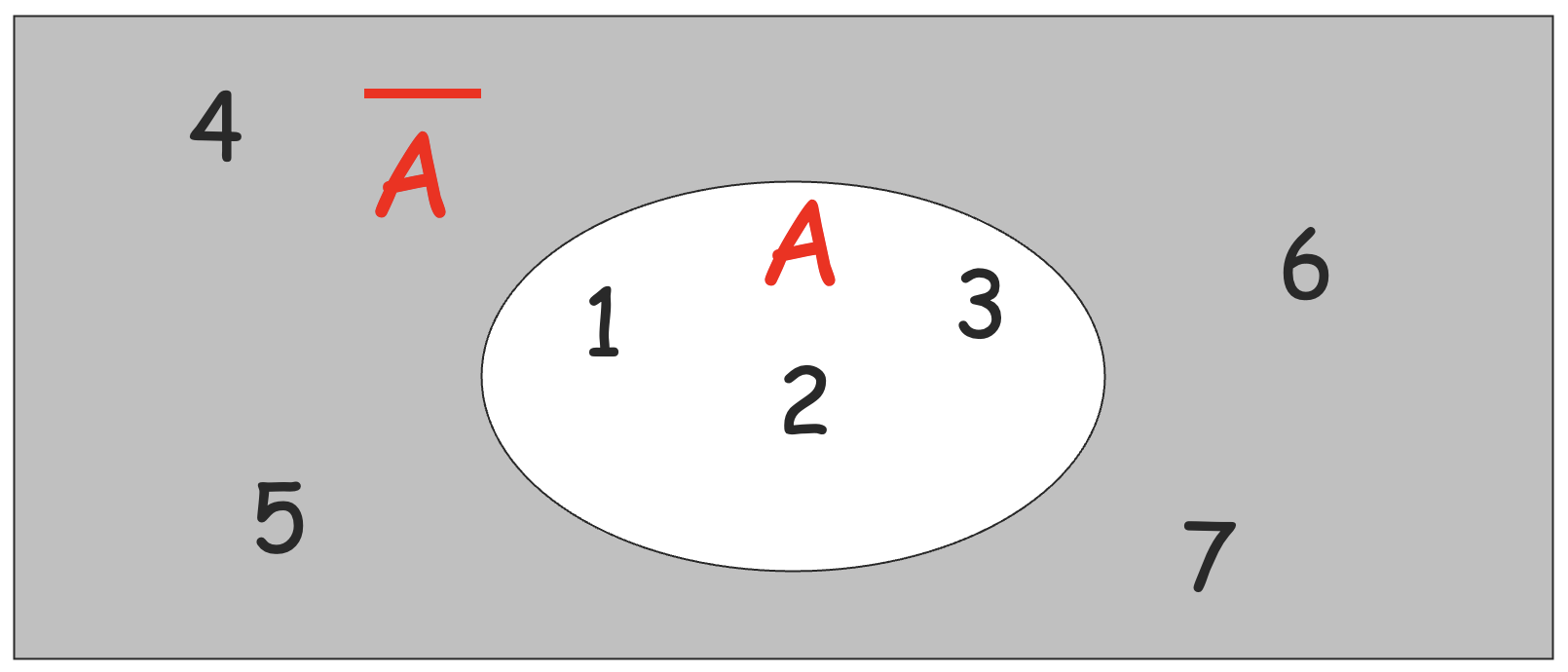
- A=A
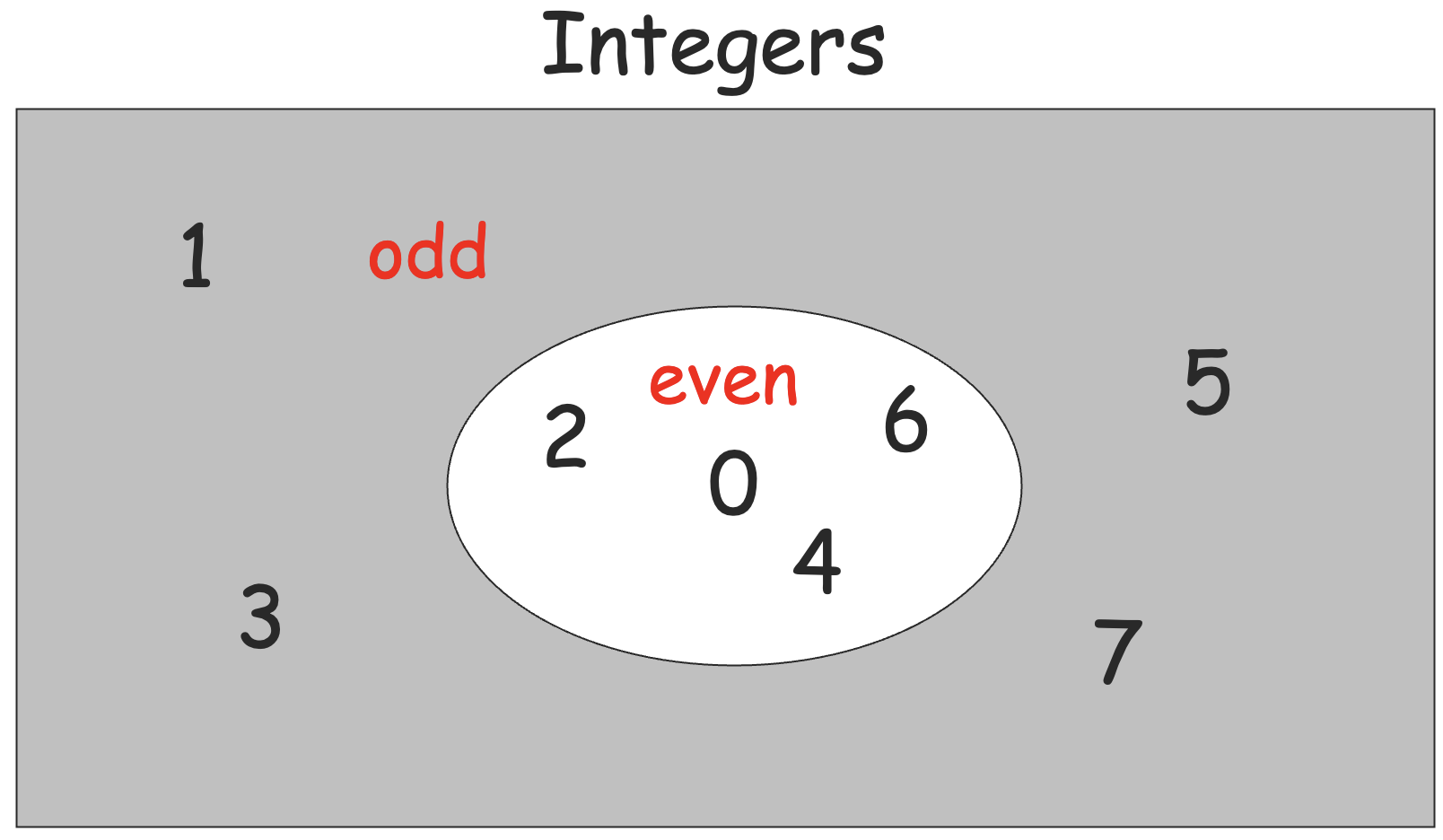
- even integers=odd integers
A∪B=A∩B
A∩B=A∪B
空集是没有任何元素的集合,写作 ∅={}。
- S∪∅=S
- S∩∅=∅
- S−∅=S
- ∅−S=∅
- ∅=U,其中 U 是全集。
例如 A={1,2,3},B={1,2,3,4,5},则:
- A⊆B,A 是 B 的子集 (subset);
- A⊂B,A 是 B 的真子集 (proper subset);
例如 A={1,2,3},B={5,6},有 A∩B=∅,称 A 与 B 是不相交的集合 (disjoint sets)。
对于有限集 A={5,6,7},有 ∣A∣=3,集合的势说的是集合的大小。
幂集是集合的集合,一个集合 S 的幂集是 S 的所有子集组成的集合,记为 P(S) 或 2S。
比如 S={a,b,c},有
2S={∅,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}
并且,我们可以观察到:∣2S∣=2∣S∣,这本质上就是子集的个数公式。
例如 A={2,4},B={2,3,5},则
A×B={(2,2),(2,3),(2,5),(4,2),(4,3),(4,5)}
不难发现 ∣A×B∣=∣A∣×∣B∣。
笛卡尔积是两个集合中元素组成的有序对的集合,我们可以更一般地定义 A1×A2×...×An。
给定两个集合 A 和 B,一个从 A 到 B 的函数将 A 中的每一个元素 a 关联到 B 中的最多一个元素 b,记作 f:A→B,其中,称有对应关系的 A 中元素的集合为定义域 (domain),B 中元素的集合为值域 (range)。
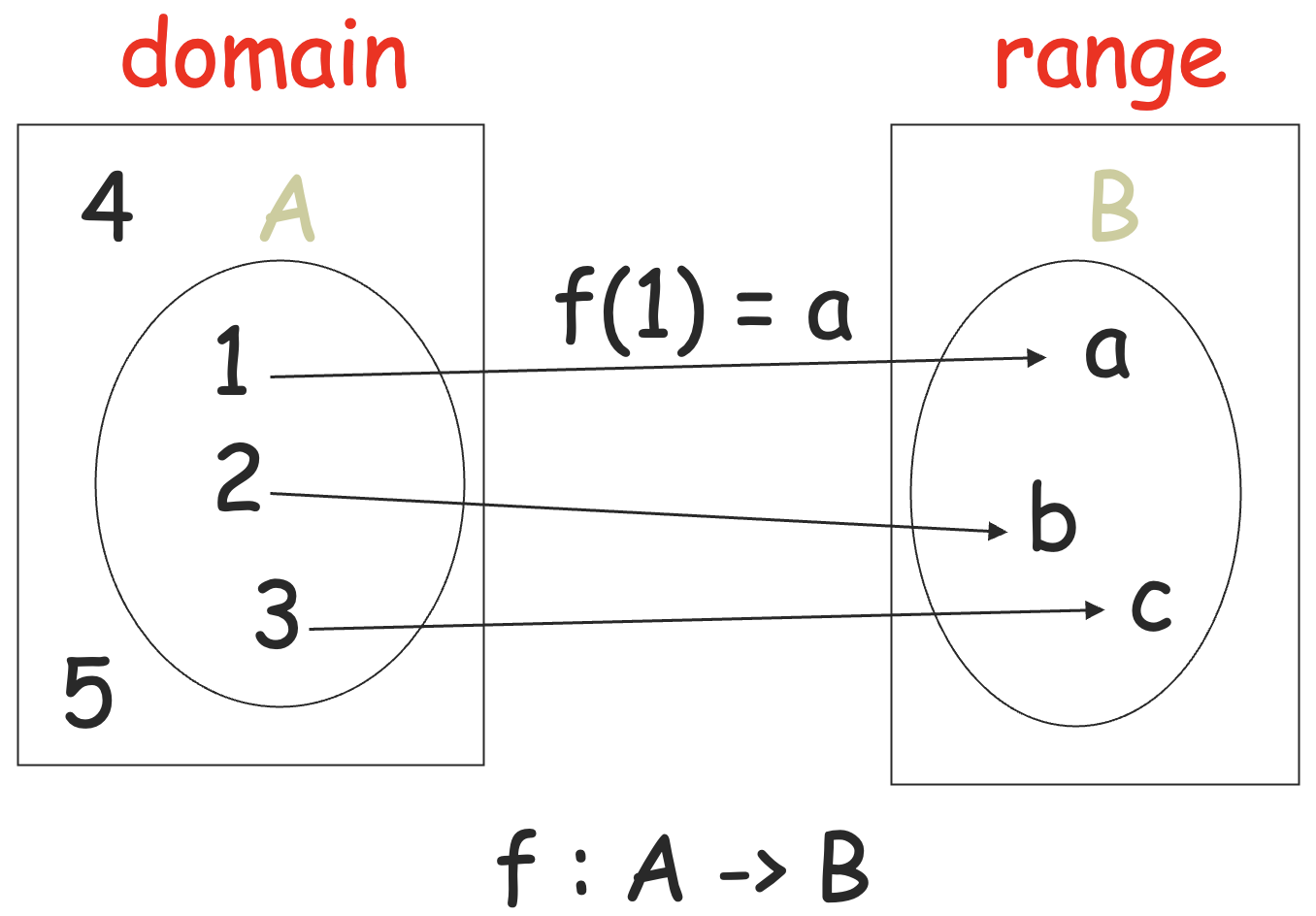
如果 A=domain,称 f 是一个全函数 (total function),否则称 f 是一个偏函数 (partial function)。
称 f:A→B 是一个双射 (bijection),如果:
- f 是全函数;
- a1=a2∈A⇒f(a1)=f(a2)
- ∀b∈B,∃a∈A,f(a)=b
双射也称为一一对应。
给定两个全函数 f,g:N→N,
一个关于集合 A1,A2,...,An 的 n 元关系 R 是 A1×A2×...×An 的子集。
给定两个集合 A 和 B,一个关系 R 是 A×B 的一个子集,即 R⊆A×B。
R={(x1,y1),(x2,y2),(x3,y3),...}
(xi,yi)∈R 可以写作 xiRyi,比如说如果 R=′>′,可以写 2>1,3>2,3>1。
- 自反性 (reflexive):xRx
- 对称性 (symmetric):xRy⇒yRx
- 传递性 (transitive):xRy∧yRz⇒xRz
比如说 = 关系是一个等价关系。
对于一个等价关系 R,定义 x 的等价类为
[x]R={y:xRy}
比如说,
R={(1,1),(2,2),(1,2),(2,1),(3,3),(4,4),(3,4),(4,3)}
则有 [1]R={1,2},[3]R={3,4}。
再比如整数集可以按照模 5 的关系分成 5 个等价类:
{{0,5,10,...},{1,6,11,...},{2,7,12,...},{3,8,13,...},{4,9,14,...}}
字符串长度可以被用来划分所有的比特串:
{{},{0,1},{00,01,10,11},{000,...,111},...}
令 R 是 A 上的一个等价关系,则对于 ∀a,b∈A,[a]R=[b]R∨[a]R∩[b]R=∅。
称集合 A 上满足自反性,传递性与反对称性 (antisymmetric) 的二元关系 R 为偏序关系 (partial order)。
称集合 A 上满足 ∀a,b∈A,aRb∨bRa 的偏序关系为全序关系 (total order)。
全序也称之为线性序 (linear order),因为具有全序关系 R 的集合 A 中的元素可以排成一行,满足 a 在 b 的左边当且仅当 aRb。
一个有向图 (directed graph) G=(V,E):
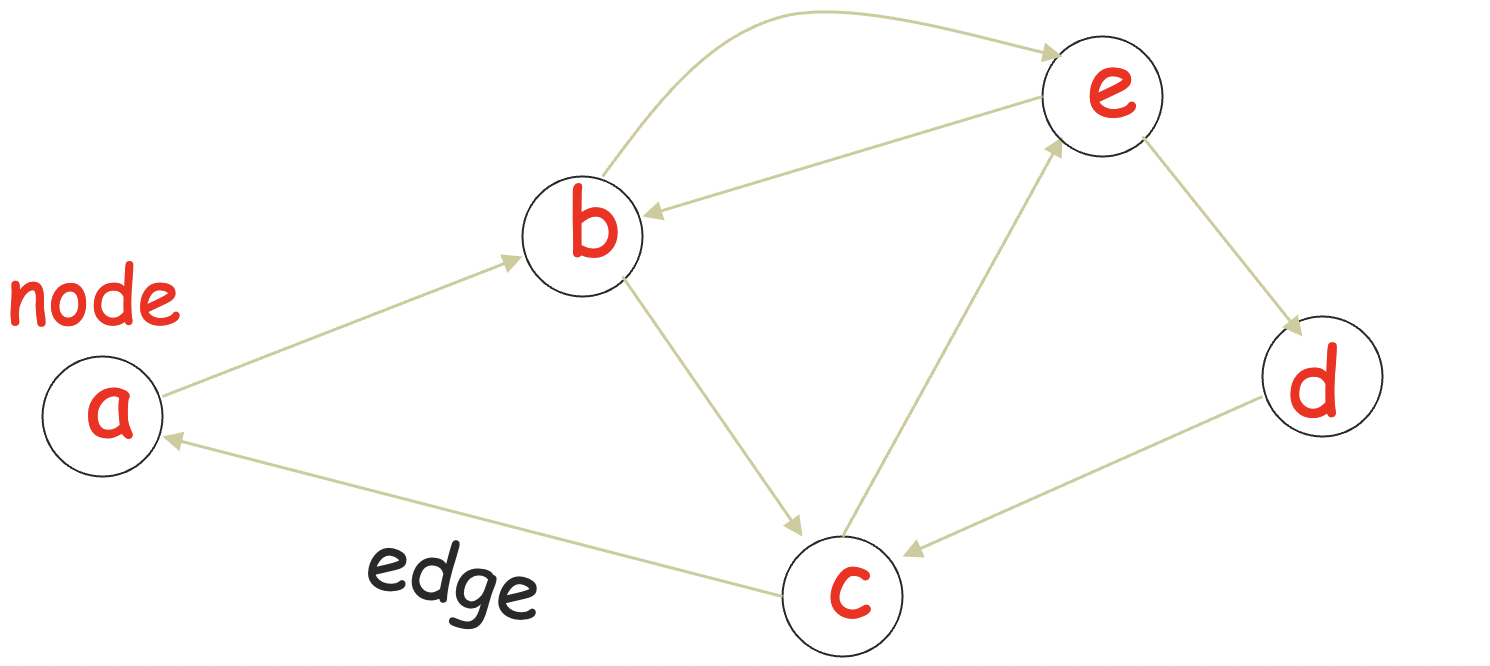
结点 (nodes / vertices) 集 V
V={a,b,c,d,e}
边 (edges) 集 E
E={(a,b),(b,c),(b,e),(c,a),(c,e),(d,c),(e,b),(e,d)}
为所有边打上标签的图称为标记图。
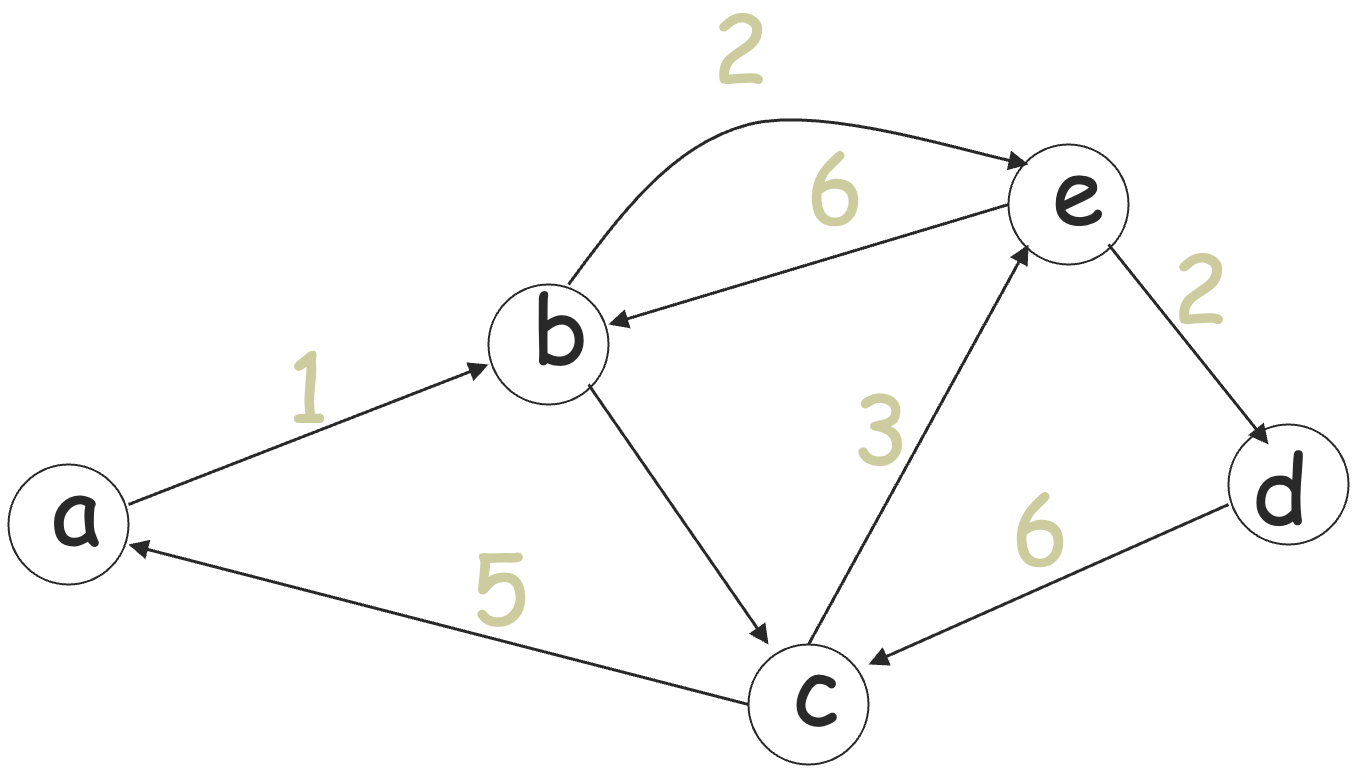
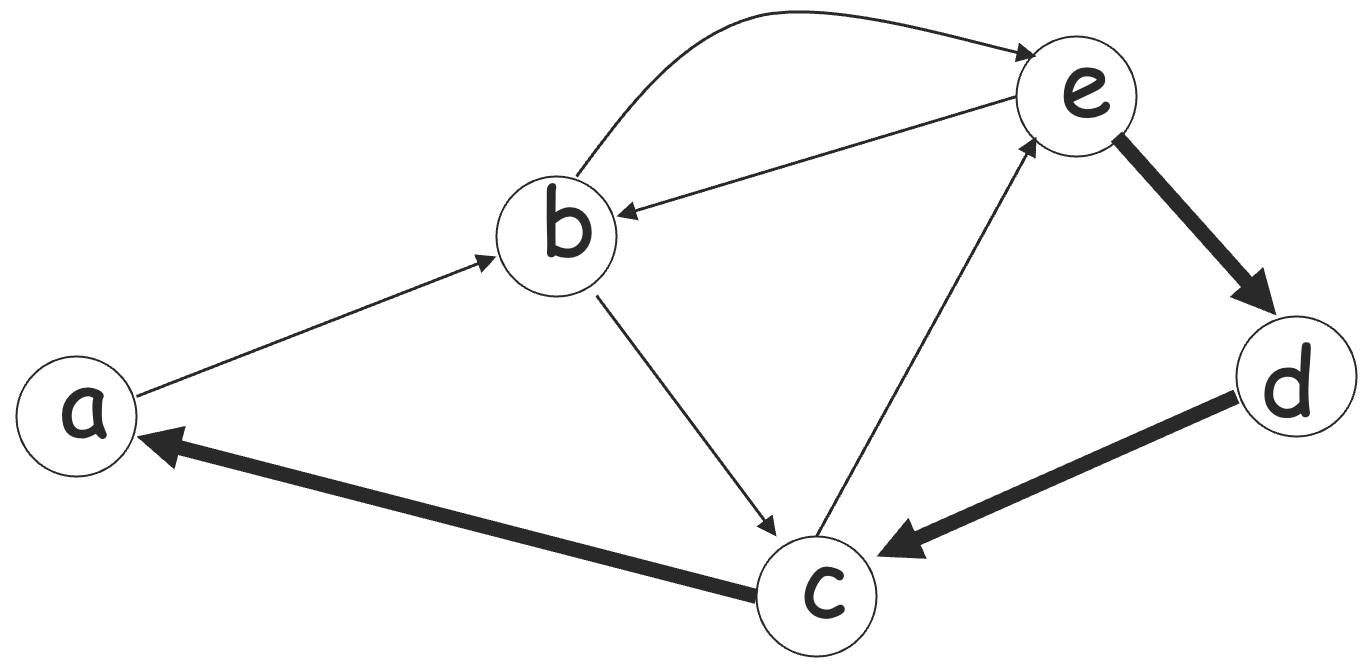
游走是一系列相邻的边:
(e,d),(d,c),(c,a)
路径是没有重复边的游走,简单路径 (simple path) 是没有重复结点的路径。
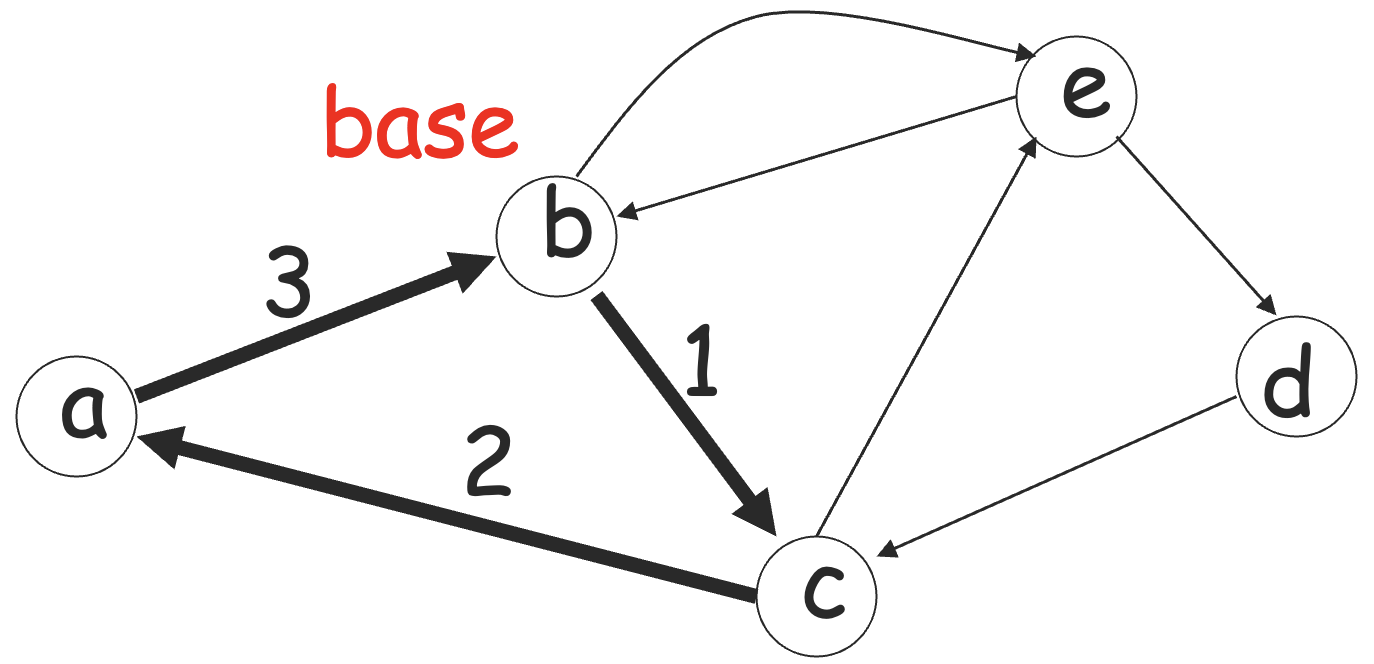
环是从一个结点(称为基础结点 base node)到它本身的游走,简单环是只有基础结点重复的环。
给定有向图 G=(V,E) 以及结点 u,v,称 v 从 u 可达,或者 u -可达,如果存在从 u 到 v 的路径。
树是一个没有环(无向环)的有向图。
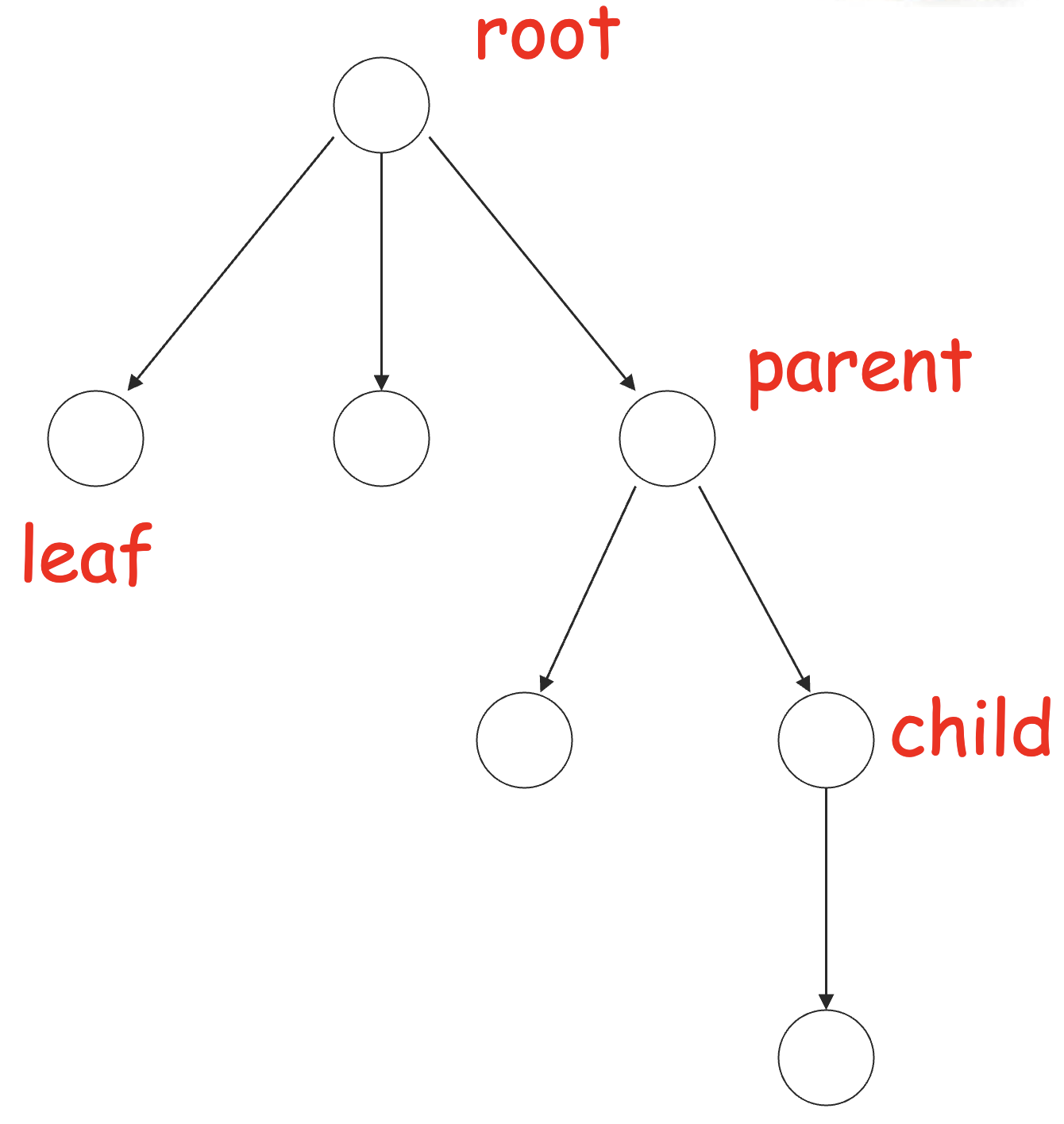
入度为 0 的结点是根结点 (root),出度为 0 的结点是树叶 (root),边总是从父母 (parent) 结点指向孩子 (child) 结点。
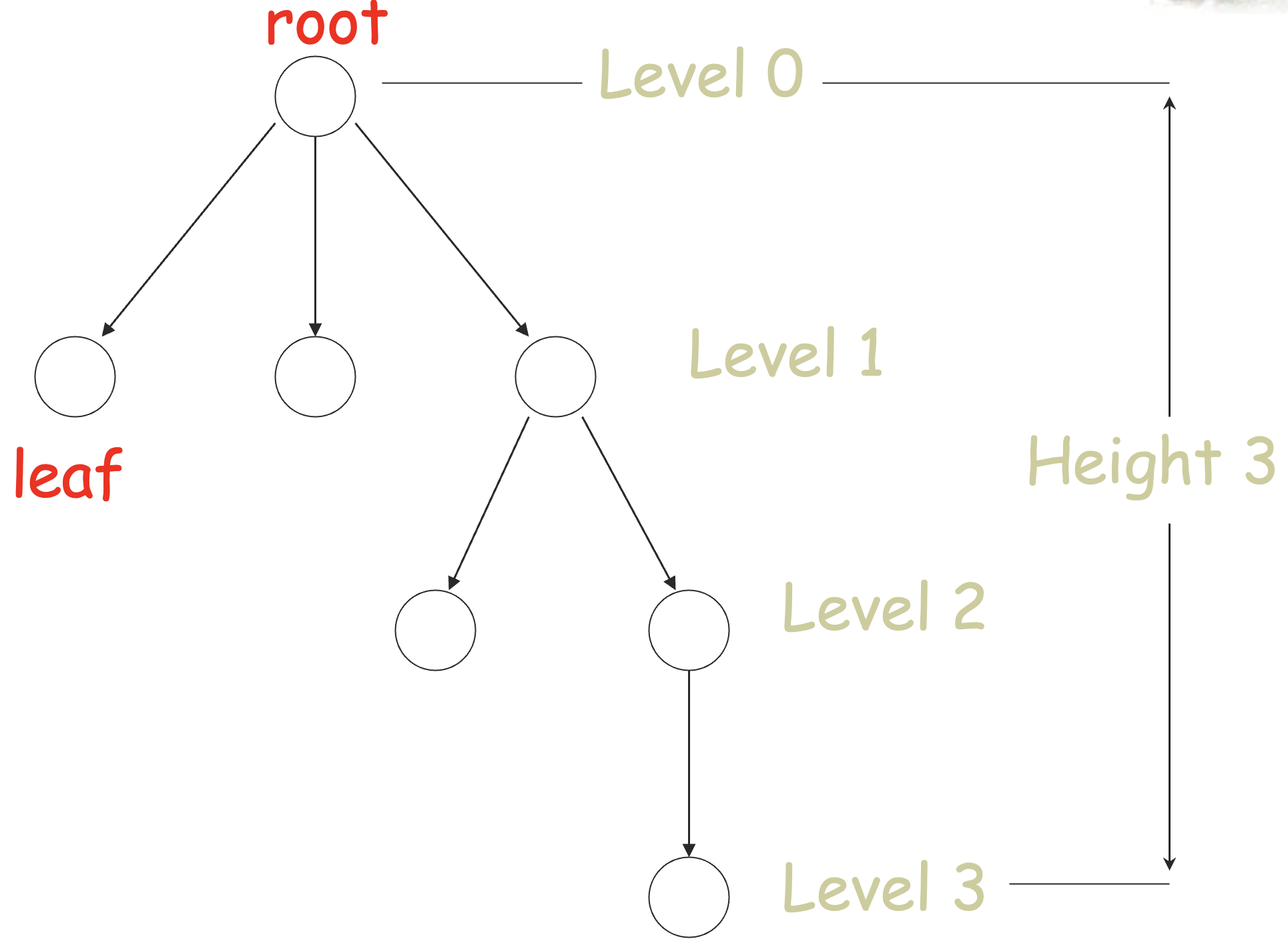
定义树上最长的路径的长度为树的高度 (height),从根结点到某结点的路径的长度为该结点的层 (level)。
有命题 P1,P2,P3,...,如果我们知道:
- 对于某个 b,P1,P2,...,Pb 是真的;
- ∀k≥b,P1∧P2∧...∧Pk⇒Pk+1; 则有 ∀i,Pi。
想要证明命题 P 为真:
- 假设 P 为假;
- 然后发现矛盾;
- 从而 P 只能为真。
如果 n+1 个物品被放倒了 n 个盒子里面,至少有一个盒子包含了至少 2 个物品。
可用反证法证明。
- 语言 (language) 是字符串 (string) 的集合。
- 字符串是一个字母 (letter) 或者符号 (symbol) 的序列 (sequence)。
- 例如:
cat,dog,house,... - 符号是由一个字母表 (alphabet) 定义的:
Σ={a,b,c,...,z}
如果 Σ={a,b},那么基于这个字母表可以有的字符串有:a,ab,abba 等等。
一般我们会用 u、v、w 之类的字母表示字符串,比如说 u=ab,v=bbbaaa,w=abba。
记 w=a1a2...an,v=b1b2...bm,定义如下一些字符串操作:
- 拼接 (concatenation)
- wv=a1a2...anb1b2...bm
- 翻转 (reverse)
- wR=an...a2a1
- 长度 (length)
- ∣w∣=n
- ∣uv∣=∣u∣+∣v∣
- 空串 (empty string)
- 用 λ 或者 ε 表示
- ∣λ∣=0
- λw=wλ=w
- 子串 (substring)
- s 是 x 的子串,如果存在字符串 y,z 使得 x=ysz。
- 子串是原字符串的子序列。
- 前缀与后缀
- 当 x=sz 即 y=ε 时,称 s 是 x 的一个前缀 (prefix);
- 当 x=ys 即 z=ε 时,称 s 是 x 的一个后缀 (suffix)。
- 重复 (repetition)
- wn=ww...w ( n 个相同的字符串拼接 )
- 定义 w0=λ
练习
解方程:011x=x011。提示:对 x 的长度分类。
辨析一些记号的含义:
- 集合:∅={}={λ}
- 集合的势:
- ∣{}∣=∣∅∣=0
- ∣{λ}∣=1
- 字符串长度:
有了上面的定义与记号之后,我们后续定义语言就方便多了。比如说 L={anbn:n≥0},则 λ∈L,ab∈L,aabb∈L,aaaaabbbbb∈L,但 abb∈/L。
- 通常的集合操作:
- {a,ab,aaaa}∪{bb,ab}={a,ab,bb,aaaa}
- {a,ab,aaaa}∩{bb,ab}={ab}
- {a,ab,aaaa}−{bb,ab}={a,aaaa}
- 补集 (complement):L=Σ∗−L
- 例如:{a,ba}={λ,b,aa,ab,bb,aaa,...}
- 翻转 (reverse):LR={wR:w∈L}
- 例如:L={anbn:n≥0},LR={bnan:n≥0}
- 拼接 (concatenation):L1L2={xy:x∈L1,y∈L2}
- 例如:{a,ab,ba}{b,aa}={ab,aaa,abb,abaa,bab,baaa}
- 语言的拼接和字符串的拼接不一样,它的组合方式同笛卡尔积。
- 多重拼接:Ln=LL...L,等号右边共有 n 个语言的拼接。
- 例如:{a,b}3={a,b}{a,b}{a,b}={aaa,aab,aba,abb,baa,bab,bba,bbb}
- 特殊情况:L0={λ}
- 星闭包 (star-closure, kleene):L∗=L0∪L1∪L2∪...
- 例如:{a,bb}∗={λ,a,bb,aa,abb,bba,bbbb,aaa,aabb,abba,abbbb,...}
- 正闭包 (positive-closure):L+=L∗−{λ}












